Data sets, Code, and Tools

Introduction

The aim of this web page is to provide data sets and elementary codes to researchers working on discrete geometry and mathematical morphology. The idea is to make it easy for the community to try our own algorithms on the same image examples as other researchers, as well as to try the algorithms of other researchers. Obviously, feel free to send an e-mail to authors of these web pages (see below) if you have comments.

Table of content:

  • Data sets: A collection of copyright free 2d and 3 images
  • Code: Libraries and code for many common methods in discrete geometry and mathematical morphology
  • Tools: Tools for common problems in discrete geometry and mathematical morphology

You think that your data set, code or tool should be listed here: just send a mail to tc18@tc18.org

Data sets

Note : all the materials present in these web pages are copyright free.

Code

Libraries

Description Main Reference Language Download
DGtal Digital Geometry Tools and Algorithms --- C++ go
HIGRA Hierarchical Graph Analysis [Perret 2019] C++/Python go
OLENA Image processing, image recognition, and artificial vision --- C++ go
ORFEO Optical and Radar Federated Earth Observation --- C++ go
PINK PINK Image Processing Library --- C++ go
VIGRA Vision with Generic Algorithms --- C++ go

Grid, cells, structures and topology

and basic librairies to handle discrete objects...
Description Main Reference Language Download Snapshots Submitted by
Simplevol a simple and powerful library to manipulate 3D images --- C++ go see 3D data set web page D.Coeurjolly
The Npic library provides types and functions in C language to manipulate bitmap images of dimension 2 to 6, and command line tools that give access to the library functions (drawing, distance transforms, medial axis, converting file formats, and more). Some computations are multi-threaded with OpenMP. --- C go   E. Thiel
Skeletonization for 2D binary data by curvature --- C go   A. Imiya
Boundary Extraction for 3D binary image by Distance Transformation --- C go A. Imiya

See also:

  • QVox in the Miscellaneous section (implementation of thinning algorithms)

nD objects and recognition

Description Main Reference Language Download Snapshots Submitted by
Multigrid discrete volume generator with signature (area, curvature...) based on Libvol --- C++ go see 3D data set web page D.Coeurjolly
Discrete Straight Line Segmentation based on Debled and Reveillès DSL [DEBLED 1995] C debled.c D.Coeurjolly
Digital plane recognition and digital plane preimage computation --- C go D.Coeurjolly
Thick Line Segment Detection with Fast Directional Tracking [Even 2019] C++ go 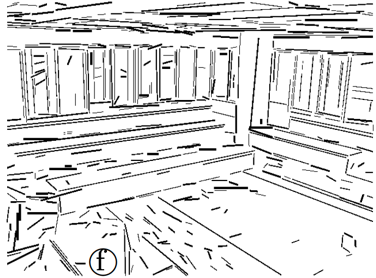P. Even

Discrete distances and skeletons

Description Main Reference Language Download Snapshots Submitted by
hLutChamfer3D is a two-phase method that determines if a G-symmetrical chamfer mask induces a norm and in this case, computes the lookup tables and the test neighborhood based on geometric properties of the chamfer balls. [Normand_2008] C go N. Normand
Program to compute optimal coefficients of 3-D chamfer norms. [FOUARD 2005] JAVA go C. Fouard G. Malandain
[FOUARD 2005] [MALANDAIN 2005] C go G. Malandain C. Fouard
3D Squared Euclidean Distance Transform in optimal time [SAITO 1994], [HIRATA_1996] and [MEIJSTER 2000] C++ go D. Coeurjolly
3D Discrete Voronoi diagram computation [SAITO 1994], [HIRATA_1996] and [MEIJSTER 2000] C++ go D. Coeurjolly

See also:

Features extraction and similarity measures

See also:

Miscellaneous

Description Main Reference Language Download Snapshots Submitted by
QVox: A 3d volumetric data visualizer with some homotopic thinning algorithms. --- C go S. Fourey

Tools on the web

  • Visualization tools
    • QVox: A 3d volumetric data visualizer written by Sébastien Fourey (see the TC18 code web page).
    • Geomview: an simple interactive 3D viewing program for Unix. Major advantages are : easy to use input format (close to VRML), postscript snapshots, export to VRML. See the 3-D data code web page for snapshots.
    • VRML: web based visualization tool.
  • Computational Geometry tools
    • qhull : Qhull computes convex hulls, Delaunay triangulations, halfspace intersections about a point, Voronoi diagrams, furthest-site Delaunay triangulations, and furthest-site Voronoi diagrams. It runs in 2-d, 3-d, 4-d, and higher dimensions. It implements the Quickhull algorithm for computing the convex hull. Qhull handles roundoff errors from floating point arithmetic. It computes volumes, surface areas, and approximations to the convex hull. Export to Geomview avaliable.
    • Computational Geometry center: useful links and tools about computational geometry.

References

  • Debled-Rennesson, I., & Reveillès, J. P. (1995). A linear algorithm for segmentation of digital curves. International Journal of Pattern Recognition and Artificial Intelligence, 9(04), 635-662.
  • Even, P., Ngo, P., & Kerautret, B. (2019, September). Thick Line Segment Detection with Fast Directional Tracking. In International Conference on Image Analysis and Processing (pp. 159-170). Springer, Cham.
  • Fouard, C., & Malandain, G. (2005). 3-D chamfer distances and norms in anisotropic grids. Image and Vision Computing, 23(2), 143-158.
  • Hirata, T. (1996). A unified linear-time algorithm for computing distance maps. Information processing letters, 58(3), 129-133.
  • Malandain, G. and Fouard, C. (2005). On optimal chamfer masks and coefficients. Research Report 5566, INRIA
  • Meijster, A., Roerdink, J. B., & Hesselink, W. H. (2002). A general algorithm for computing distance transforms in linear time. In Mathematical Morphology and its applications to image and signal processing (pp. 331-340). Springer, Boston, MA.
  • Normand, N., & Evenou, P. (2009). Medial axis lookup table and test neighborhood computation for 3D chamfer norms. Pattern Recognition, 42(10), 2288-2296.
  • Perret, B., Chierchia, G., Cousty, J., Guimarães, S. J. F., Kenmochi, Y., & Najman, L. (2019). Higra: Hierarchical graph analysis. SoftwareX, 10, 100335.
  • Saito, T., & Toriwaki, J. I. (1994). New algorithms for euclidean distance transformation of an n-dimensional digitized picture with applications. Pattern recognition, 27(11), 1551-1565.